III. Codage d’une image et calcul du poids



La profondeur de couleur :

Les images sont codées d'une certaine façon de manière à ce qu'elle soit comprise par l'ordinateur.
Voyons d’abord qu'est ce qu'un bit :

Le bit est la plus petite unité de stockage en informatique. Un bit peut coder deux états, il peut prendre 2 valeurs : 0 ou 1 (état vrai ou faux) : nous sommes donc en présence d'un système binaire.


8 bits = 1 octet

Un octet est formé de 8 bits. Vu que l'on est en système binaire, il est donc facile de calculer le nombre de possibilités pour un octet : 28 soit 256 états possibles.

La profondeur de couleur (exprimé en bit) est plus communément appelée « Nombre de bits par pixel ». Plus elle est importante, plus l'image peut afficher de couleurs différentes. La profondeur de couleur d'une image bitmap peut être de 1, 4, 8 ou encore 24 bpp (bits par pixel).


Bits par pixel 1 4 8 24
Nombre de couleurs 2 16 256 16,7 millions


Pour notre image nous pouvons donc choisir la palette de couleur que l'on souhaite :
Avec un codage de 1 bit par pixel, on aura le choix entre 2 couleurs (par exemple une image en noir et blanc)
Avec un codage de 4 bit par pixel, on aura le choix entre 24 =16 couleurs.
Avec une image de 8 bits par pixel, on aura le choix entre 28 = 256 couleurs.
Avec une image de 24 bits par pixel, on aura le choix entre 224 = 16,7 millions couleurs.
La palette de couleur peut très bien être un dégradé de gris, de rouge, de vert.

Nous allons donc étudier le mode de codage le plus couramment utilisé pour les images numériques : le codage RVB qui est définie par :
  1. L'intensité du rouge
  2. L'intensité du vert
  3. L'intensité du bleu

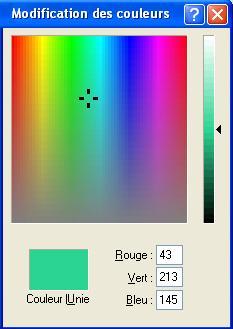
Sur cette image, nous avons 43 de rouge, 213 de vert et 145 de bleu. L'association de ces informations indique à l'ordinateur d'afficher une couleur bleu-vert.


Le principe repose sur la synthèse additive des couleurs : on peut obtenir une couleur quelconque par addition de ces 3 couleurs primaires en proportions convenables. On obtient ainsi 256 x 256 x 256 = 16777216 (plus de 16,7 millions de couleurs différentes). Donc ceci est vrai si nous sommes en présence d'un codage de 24 bpp.


Cacul du poids d'une image :
Maintenant il nous est donc facile de calculer le poids d'une image si l'on connait son codage et sa taille grâce a la relation :
Taille = (Hauteur x largeur x bpp)/8
hauteur et largeur exprimée en pixels, la taille sera alors exprimé en octets.

script réalisé par Mathias, Moshé et Sébastien
Veuillez spécifier hauteur (en pixels) largeur (en pixels) bits par pixel

L'image fera octets soit Ko ou encore Mo.

(1 Ko = 1024 octets, 1 Mo = 1024 Ko)


Exemple : Soit une image de 24 bpp (bit par pixels) de 10 cm x 10 cm et une réslution de 100 pixels par cm :
On a donc un choix de 16, 7 millions de possibilités de couleurs différentes soit 256 niveaux de rouge, 256 niveaux de vert, 256 niveaux de bleu. (256 x 256 x 256 = 16777216).
Or nous savons qu'un octet est égal à 28 = 256 possibilités donc chaque couleur est codée sur un octet.
Ce qui veut dire que pour un pixel, il faudra 3 octets pour le définir.
En résumé : En 24 bpp, chaque couleur codée sur 1 octet = 8 bits. Chaque pixel sur 3 octets.
Dans le cas de notre image (10 cm x 10 cm avec une résolution de 100 pixels par cm).
Elle comporte donc : (10 x 100) x (10 x 100) = 1000 x 1000 = 1 000 000 pixels.
L'image de 1 000 000 pixels ainsi codée occupe 1 000 000 x 3 = 3 000 000 octets = 2929,6875 Ko = 2,861 Mo.

Pour une image codée en 24 bpp on pourra donc calculer approximativement le poids d'une image en utilisant la relation suivante : la taille est exprimée en octets

Taille = Hauteur x largeur x 3

Conclusion :
Nous pouvons remarquer que les images prennent une place importante sur le disque dur, c'est pourquoi certains autres codages ont été développés. Notamment les jpeg, qui se basent sur des images à points tel que l'on a vu et qui ensuite les compressent selon un alogrithme spécifique.