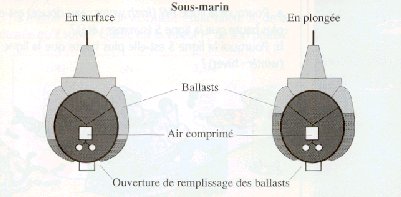
1) LES SOUS-MARINS :
a) Les origines
On attribue la paternité du premier sous-marin au Hollandais Cornelis Drebbel ( 1972-1633 ), physicien installé à la cour du roi d'Angleterre Jacques 1er et précepteur des enfants du souverain. En fait, il ne fit qu'appliquer les idées du mathématicien anglais William Bourne, énoncées dès 1578, qui définissent le principe des ballasts. C'est en 1624 que Drebbel construisit son premier submersible qu'il essaya dans la Tamise. Notons par ailleurs, que Drebbel ait eu l'idée de régénérer chimiquement l'air à bord, grâce à une solution alcaline. Bien qu'ayant au départ une vocation scientifique, le sous-marin deviendra surtout durant la seconde guerre mondiale une arme de guerre.
b) FonctionnementBien que les sous-marins aient évolué, le principe est toujours
resté le même : un sous-marin est constitué d'une double
coque : les deux coques sont séparées par un vide qui sera comblé
par l'eau. En effet, un sous-marin vidé de ces capacités navigue
à la surface ; pour qu'il puisse plonger, celui-ci fait pénétrer
de l'eau dans les ballasts. En se remplissant le sous-marin s'alourdit et commence
alors son immersion. Pour remonter il faut envoyer de l'air comprimé
dans les ballasts pour vider l'eau, ainsi la poussée d'Archimède
devient supérieure au poids de l'ensemble.

c) Applications du principe d'Archimède
Le principe d'Archimède énonce que tout corps plongé
dans un fluide subit une poussée verticale ascendante égale au
poids du volume du fluide déplacé. La poussée d'Archimède
résulte des forces exercées par le ou les fluides sur la surface
du solide immergé. Chaque élément de surface du solide
subit une force pressante ou force d'action. Cette force est l'association d'un
vecteur force
®
p et d'un point d'application
C, appelé centre de poussée.
®
Le vecteur force p est vertical
et orienté vers le haut, sa valeur correspond au poids du fluide déplacé
: p = P' = m'g = rgV, où
m' est la masse du fluide déplacé, g l'accélération
de la pesanteur au point C, r la masse volumique du liquide et V le volume du
fluide déplacé.
Notons par ailleurs, que les forces dues à la pression de l'eau augmentent au fur et à mesure que le sous-marin descend, mais la résultante de toutes ces forces reste toujours constante quelle que soit la profondeur. Ainsi, pour que le sous-marin puisse descendre en immersion, celui-ci remplit ses ballastes et augmente ainsi sa masse : à ce moment le poids P du sous-marin devient supérieur à la force p et l'immersion débute. Si le sous-marin désire stopper sa descente, il ferme ses ballasts et se met alors à naviguer entre deux eaux. Toutefois, le sous-marin atteint une limite en profondeur car comme énoncé précédemment : plus le sous-marin descend, plus la pression augmente et arrivé à une certaine profondeur ce dernier implose sous l'effet des forces exercées par la pression sur la coque. Lorsque l'on descend de 10 mètres la pression augmente de 1 bar ( 1 bar º 1013 hPa ).

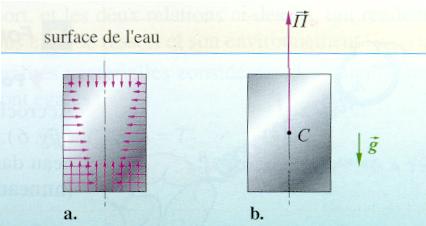
Ci-contre, les forces exercées sur le corps : son poids
(en jaune) et la résultante des forces de pression appelée la
poussée d'Archimède ( représentée en rouge et nommée
®
p ) .
Dans ce cas, les vecteurs force ont même valeur, leur résultante
est nulle donc le sous-marin est en équilibre instable (il " flotte
" entre deux eaux).